五、股票收益模型

1.导入pandas、matplotlib.pyplot和numpy

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

ms = pd.read_csv('data/microsoft.csv',index_col=0)
ms.index=pd.to_datetime(ms.index)
ms.head()

2.Log收益分布

# let play around with ms data by calculating the log daily return
ms['LogReturn'] = np.log(ms['Close']).shift(-1) - np.log(ms['Close'])
# Plot a histogram to show the distribution of log return of Microsoft's stock. 
# You can see it is very close to a normal distribution
from scipy.stats import norm
mu = ms['LogReturn'].mean()
sigma = ms['LogReturn'].std(ddof=1)

density = pd.DataFrame()
density['x'] = np.arange(ms['LogReturn'].min()-0.01, ms['LogReturn'].max()+0.01, 0.001)
density['pdf'] = norm.pdf(density['x'], mu, sigma)

ms['LogReturn'].hist(bins=50, figsize=(15, 8))
plt.plot(density['x'], density['pdf'], color='red')
plt.show()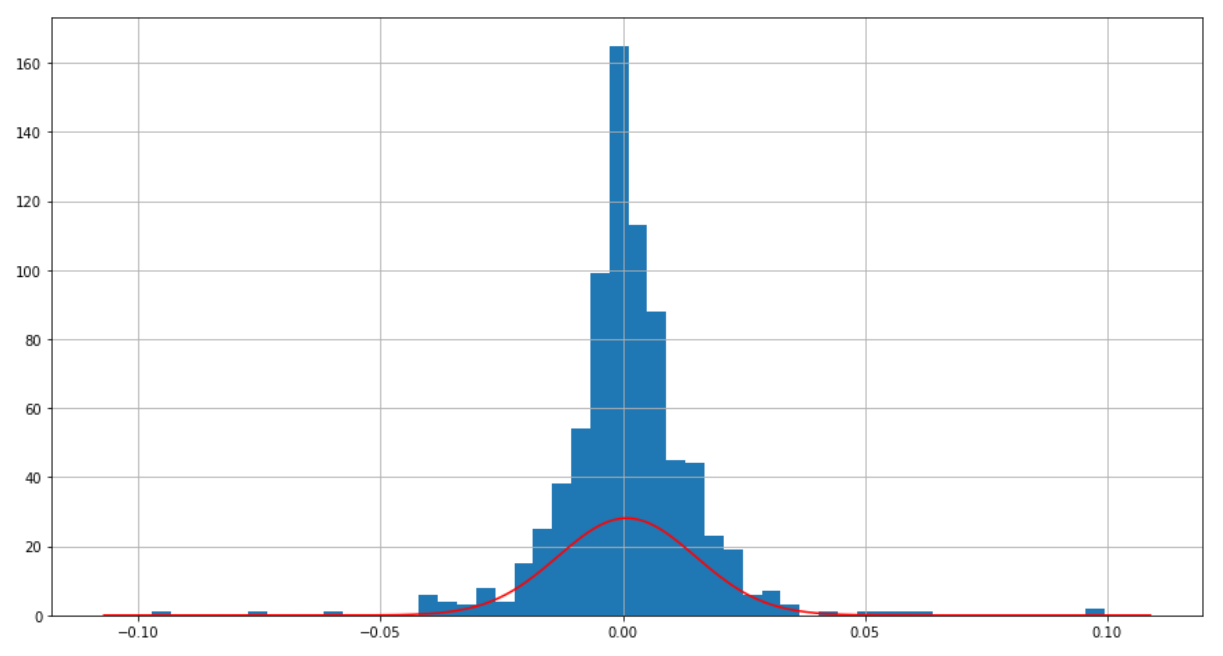

3.计算股票价格在一天内下跌超过一定百分比的概率

# probability that the stock price of microsoft will drop over 5% in a day
prob_return1 = norm.cdf(-0.05, mu, sigma)
print('The Probability is ', prob_return1)

The Probability is 0.000171184826087

# Now is your turn, calculate the probability that the stock price of microsoft will drop over 10% in a day
prob_return1 = norm.cdf(-0.10, mu, sigma)
print('The Probability is ', prob_return1)

Expected Output: The Probability is 6.05677563486e-13

4.计算股票价格在一年内下跌超过一定百分比的概率

# drop over 40% in 220 days
mu220 = 220*mu
sigma220 = (220**0.5) * sigma
print('The probability of dropping over 40% in 220 days is ', norm.cdf(-0.4, mu220, sigma220))

The probability of dropping over 40% in 220 days is 0.00291236331333

# drop over 20% in 220 days
mu220 = 220*mu
sigma220 = (220**0.5) * sigma
drop20 = None
print('The probability of dropping over 20% in 220 days is ', drop20)

Expected Output: The probability of dropping over 20% in 220 days is 0.0353523772749

5.计算风险值(VaR)

# Value at risk(VaR)
VaR = norm.ppf(0.05, mu, sigma)
print('Single day value at risk ', VaR)

Single day value at risk -0.0225233624071

# Quatile 
# 5% quantile
print('5% quantile ', norm.ppf(0.05, mu, sigma))
# 95% quantile
print('95% quantile ', norm.ppf(0.95, mu, sigma))

5% quantile -0.0225233624071
95% quantile 0.0241638253793

# This is your turn to calcuate the 25% and 75% Quantile of the return
# 25% quantile
q25 = norm.ppf(0.25, mu, sigma)
print('25% quantile ', q25)
# 75% quantile
q75 = norm.ppf(0.75, mu, sigma)
print('75% quantile ', q75)

Expected Output: 25% quantile -0.00875205783841 75% quantile 0.0103925208107