十、假设检验

import pandas as pd
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
% matplotlib inline
# import microsoft.csv, and add a new feature - logreturn
ms = pd.read_csv('data/microsoft.csv',index_col=0)
ms.index=pd.to_datetime(ms.index)
ms['logReturn'] = np.log(ms['Close'].shift(-1)) - np.log(ms['Close'])
# Log return goes up and down during the period
ms['logReturn'].plot(figsize=(20, 8))
plt.axhline(0, color='red')
plt.show()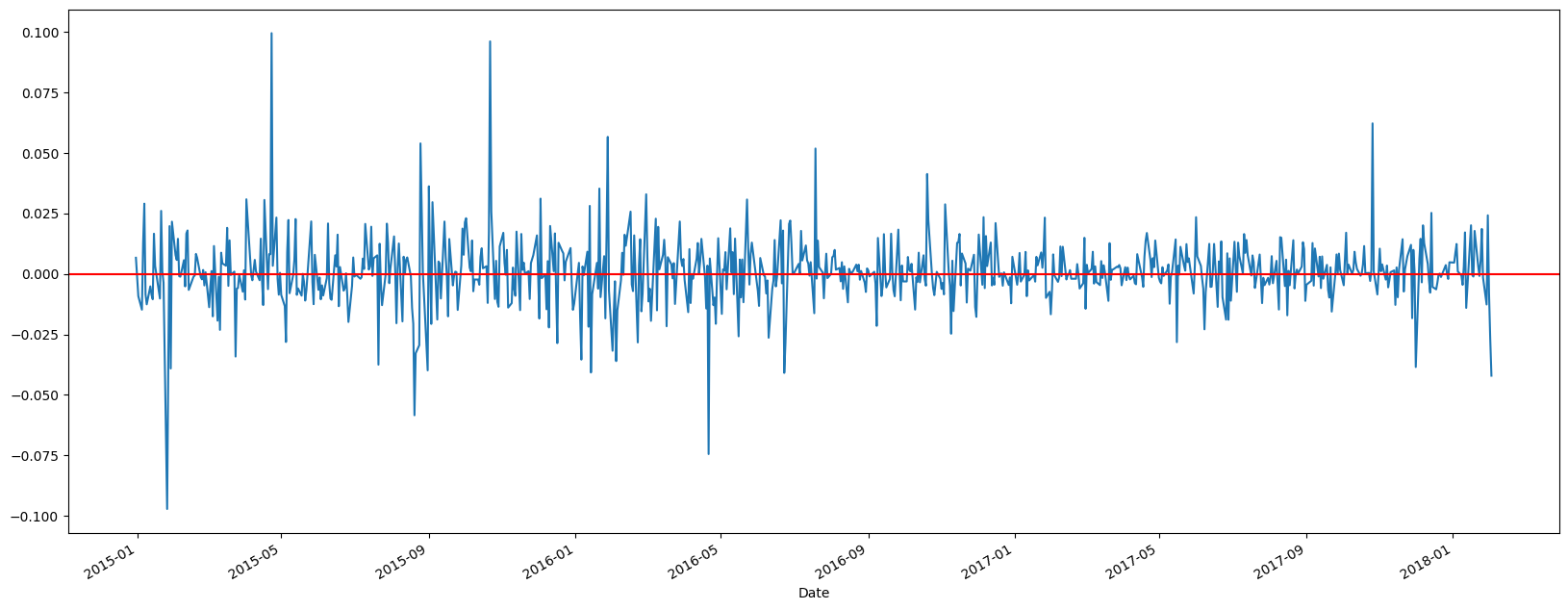

Steps involved in testing a claim by hypothesis testing

Step 1: Set hypothesis

H0 means the average stock return is 0 H1 means the average stock return is not equal to 0

Step 2: Calculate test statistic

sample_mean = ms['logReturn'].mean()
sample_std = ms['logReturn'].std(ddof=1)
n = ms['logReturn'].shape[0]

# if sample size n is large enough, we can use z-distribution, instead of t-distribtuion
# mu = 0 under the null hypothesis
zhat = (sample_mean - 0)/(sample_std/n**0.5)
print(zhat)

1.6141477140003675

Step 3: Set desicion criteria

# confidence level
alpha = 0.05

zleft = norm.ppf(alpha/2, 0, 1)
zright = -zleft  # z-distribution is symmetric 
print(zleft, zright)

-1.95996398454 1.95996398454

Step 4: Make decision - shall we reject H0?

print('At significant level of {}, shall we reject: {}'.format(alpha, zhat>zright or zhat<zleft))

At significant level of 0.05, shall we reject: False

Try one tail test by yourself !

# step 2
sample_mean = ms['logReturn'].mean()
sample_std = ms['logReturn'].std(ddof=1)
n = ms['logReturn'].shape[0]

# if sample size n is large enough, we can use z-distribution, instead of t-distribtuion
# mu = 0 under the null hypothesis
zhat = (sample_mean - 0)/(sample_std/n**0.5)
print(zhat)

Expected output: 1.6141477140003675

# step 3
alpha = 0.05

zright = norm.ppf(1-alpha, 0, 1)
print(zright)

Expected output: 1.64485362695

# step 4
print('At significant level of {}, shall we reject: {}'.format(alpha, zhat>zright))

Expected output: At significant level of 0.05, shall we reject: False

An alternative method: p-value

# step 3 (p-value)
p = 1 - norm.cdf(zhat, 0, 1)
print(p)

0.053247694997

# step 4
print('At significant level of {}, shall we reject: {}'.format(alpha, p < alpha))

At significant level of 0.05, shall we reject: False